Seandainya ada fitur latex nya kan enak juga, sekalian aku mau nulis persamaan matematik yang sederhana, dan ngerjain pertanyaan kan lebih enak jadi kayanya lebih keren jika memakai latex sebagai contoh seperti ini cuma harus bisa memakai latex? 

√x+√y+√z = 1, x,y,z adalah real positif

sifat sifat bilangan real positif :

⇒ x,y,z > 0

sehingga kita bisa mengasumsikan

⇒ 0 < x ≤ y ≤ z

jadi bisa ditambahkan berdasarkan sifat bilangan positif

⇒ x + y ≤ z + x

kalau perkaliannya jadi begini karena sifatnya positif dan seragam (cyclic)

sedemikian hingga pola perkaliannya menjadi :

xy ≤ yz ≤ zx sehingga berdasarkan sifat bilangan real positif dan cyclic sedemikian hingga

⇒ 2x²(y+z) ≤ 2y²(x+z) ≤ 2z²(y+x)

sehingga kalau dibikin pecahan sifatnya pertidaksamaannya akan terbalik kek bgini nich

⇒ [1/√(2z²(y+x))] ≤ [1/√(2y²(x+z))] ≤ [1/√(2x²(y+z))]

jadi kalau dibikin perkalian pembilang penyebut tinggal ditarik kesimpulan dari sifat2 diatas :

sama saja gak berubah pola pertidaksamaannya menjadi : 

⇒ [(xy + zx)/√(2x²(y+z))] ≤ [2yz/√2x²(y+z))]

karena sifatnya seragam tulis aja begini

⇒ ∑[(xy + zx)/√2x²(y+z))] ≤ ∑ [2yz/√2x²(y+z))].........................❶

-------------------------------------------------------------------------

⇒ [(x²+yz)/√(2x²(y+z))]+[(y²+xz)/√(2y²(x+z))]+[(z²+yx)/√(2z²(y+x))] ≥ 1

untuk memudahkan pengetikan lagi karena panjang dan seragam ditulis

disingkat begini saja :

⇒ [(x²+yz)/√(2x²(y+z))]+[(y²+xz)/√(2y²(x+z))]+[(z²+yx)/√(2z²(y+x))]=∑(x²+yz)/√(2x²(y+z))

---------------------------------------------------------------------------

⇒ ∑ (x²+yz)/√(2x²(y+z))........................................................❷

❶→❷ gabungkan

⇒ ∑[2x²+2yz/√(2x²(y+z))] ≥ ∑[2x²+xy+zx/√(2x²(y+z))]

⇒ ∑[2x²+2yz/√(2x²(y+z))] ≥ ∑[2x²+x(y+z)/√(2x²(y+z))]

⇒ ∑[2x²+2yz/√(2x²(y+z))] ≥ ∑[(2√(2x³(y + z))/√(2x²(y+z))] corat coret

⇒ ∑[2x²+2yz/√(2x²(y+z))] ≥ ∑ 2√x

⇒ ∑[2x²+2yz/√(2x²(y+z))] ≥ 2(√x+√y+√z)

⇒ ∑[2x²+2yz/√(2x²(y+z))] ≥ 2

kita ambil titik terkecilnya saja, karena kalau yang besar sudah pasti memenuhi

⇒ ∑[2x²+2yz/√(2x²(y+z))] = 2

⇒ [(x²+yz)/√(2x²(y+z))]+[(y²+xz)/√(2y²(x+z))]+[(z²+yx)/√(2z²(y+x))] = 2

⇒ 2 ≥ 1

proved

 nah maksudku pengen nulis seperti ini

 

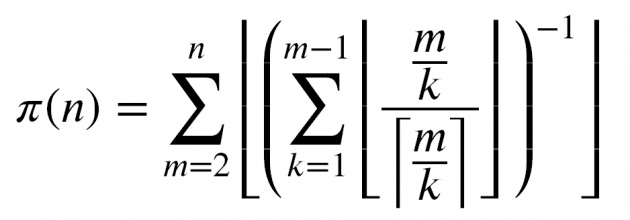
jadi kalau bisa beginian ntar anak anak kumpulan di sosial media pasti banyak kumpul disini , wah pasti bakalan seru dech , yaaah nulis latex di bitlanders memang sulit tapi tetap semangat hehe