PROBLEM#01:

Given the values of R and C, obtain the unit step response of the first order system.

i. R=2KΩ and C=0.01F     

                         

SOLUTION:

CODING

R1=2e3;

C1=0.01;

R2=2.5e3;

C2=0.003;           

num1=1;

den1=[R1*C1 1];

den2=[R2*C2 1];

sys1=tf(num1,den1);

sys2=tf(num1,den2);

step(sys1,sys2);    

legend('system1','system2');

RESULT

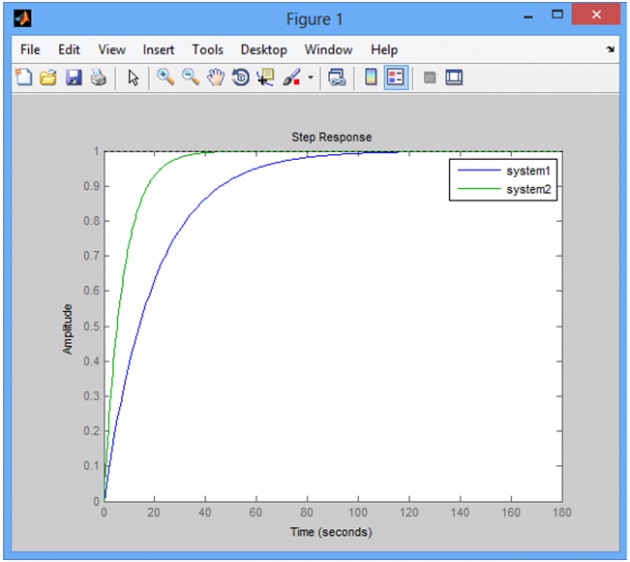
Steady State values are :

t1=R1*C1

t1 = 20

t2 = R2*C2

t2 = 7.5000

//////////////////////////////////////////////////////////////////////////////////////////

PROBLEM#02:

Effect of damping ratio ζ on performance measures. For a single-loop second order feedback system given below

SOLUTION:

a) CODING

In function window

function sys = secondordersystem(wn,zeta)

s=tf('s');sys1= (wn^2)/(s^2 + (2*zeta*wn*s) + wn^2);

sys=feedback(sys1,1);

end

 

In command window

wn=1;

zeta=0.1;  sys1=secondordersystem(wn,zeta);

zeta=0.4;  sys2=secondordersystem(wn,zeta);

zeta=0.7;  sys3=secondordersystem(wn,zeta);

zeta=1.0;  sys4=secondordersystem(wn,zeta);

zeta=2.0;  sys5=secondordersystem(wn,zeta);

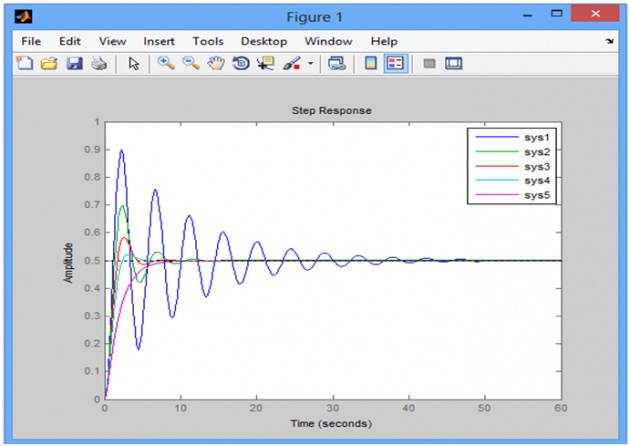
step(sys1,sys2,sys3,sys4,sys5);

legend('sys1','sys2','sys3','sys4','sys5');

 

RESULT

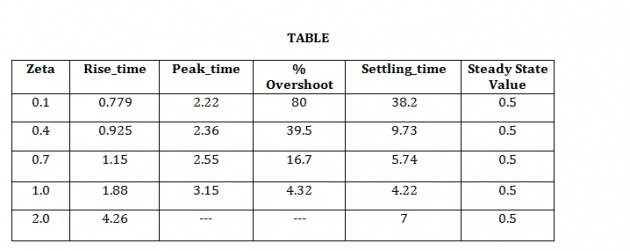
b) CODING

In command window

wn=5; zeta=0.7;

num=[0 0 wn^2];

den=[1 2*zeta*wn wn^2];

t=0:0.005:5;

[y x t]=step(num,den,t);

r=1;

while(y(r)<=0.90)

r=r+1;

 

end

t1=0.005*(r-1);

r=1;

while(y(r)<=0.10)

r=r+1;

end

t2=0.005*(r-1);

rise_time=t1-t2;

[ymaxtp]=max(y);

peak_time=0.005*(tp-1);

max_overshoot= ymax-1;

s=1000;

while(y>0.98 & y<1.02)

s=s-1;

end

settling_time=0.005*(s-1);

plot(t,y)

 

RESULT

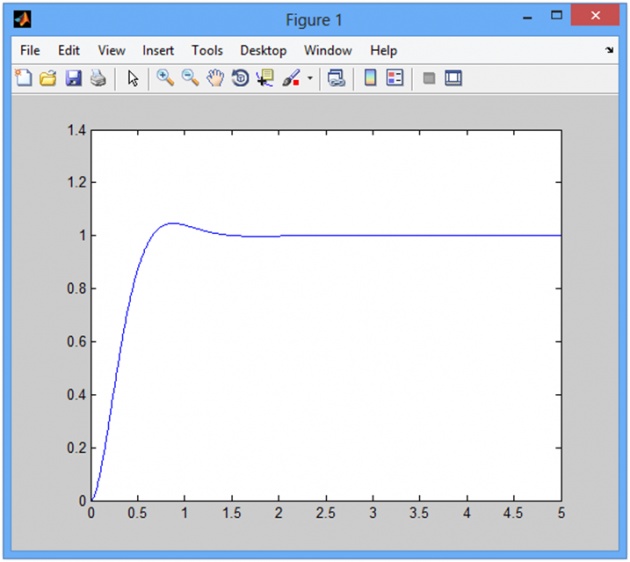
Written by: Babar Adrees

International islamic uni islamabad (iiui)