Solution

a)                  

num = [0 0 400];

den = [1 48.5 0];

plant = tf(num,den);

step(plant)

Output

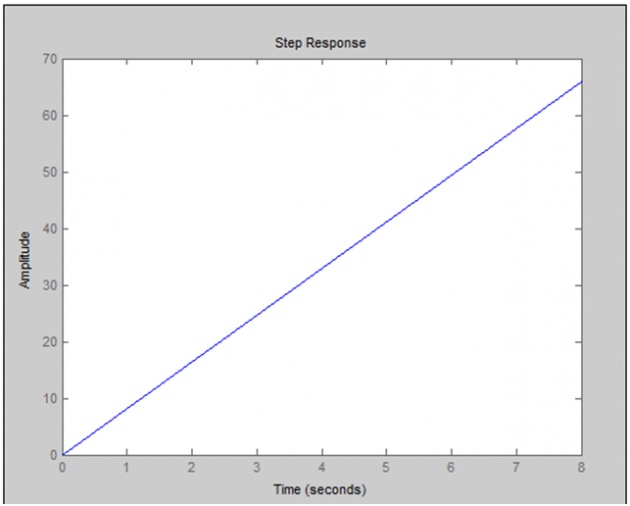
b)   

num = [0 0 400];

den = [1 48.5 0];

plant = tf(num,den);

Kp = 2;

% Kp = 10;

% Kp = 100;

Ki = Kp/10;

contr=tf([Kp Ki],[1 0]);

sys_cl=feedback(contr*plant,1);

t=0:0.01:2;

step(sys_cl,t)

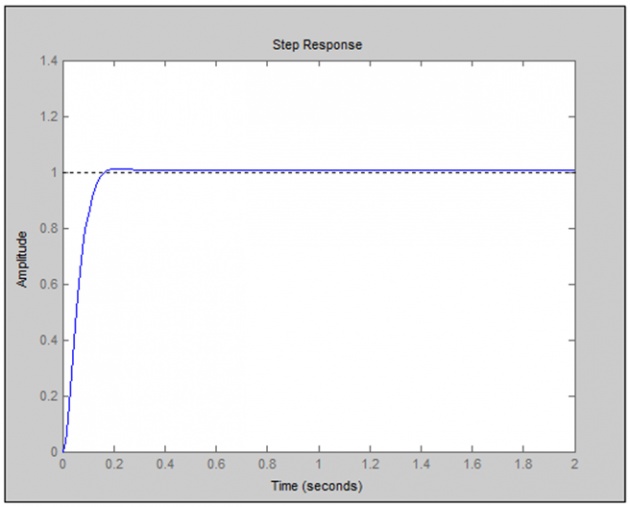
kp = 2

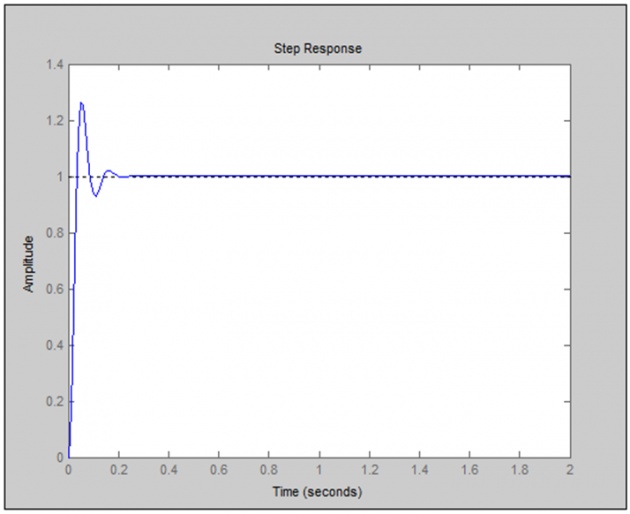
kp = 10 

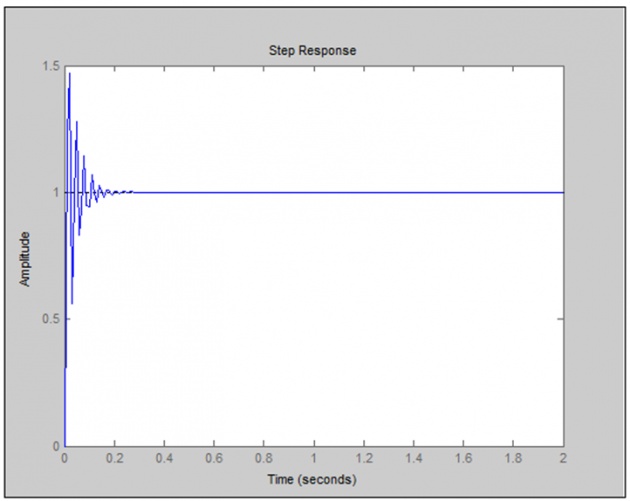
kp = 100

Result

Increasing Kp, rise time decreases , overshoot increases, Peak time also decreases .

c)   

num = [0 0 400];

den = [1 48.5 0];

plant = tf(num,den);

Kp=100;

Ki=10;

Kd=0.1;

% Kd=0.9;

% Kd=2.0;

contr=tf([KdKp Ki],[1 0]);

sys_cl=feedback(contr*plant,1);

t=0:0.01:2;

step(sys_cl,t)

kp = 0.1

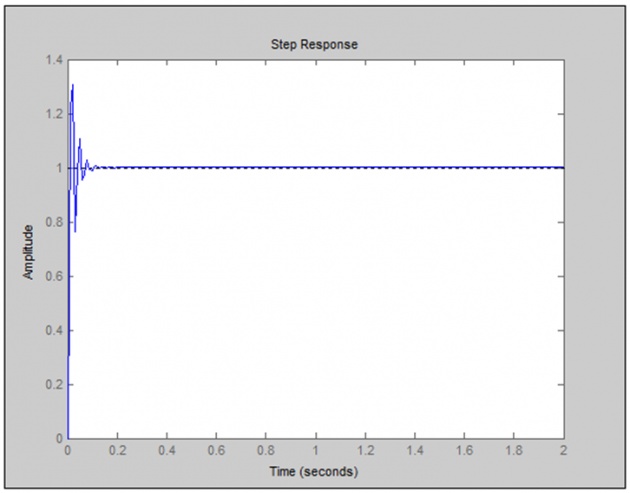
kp = 0.9

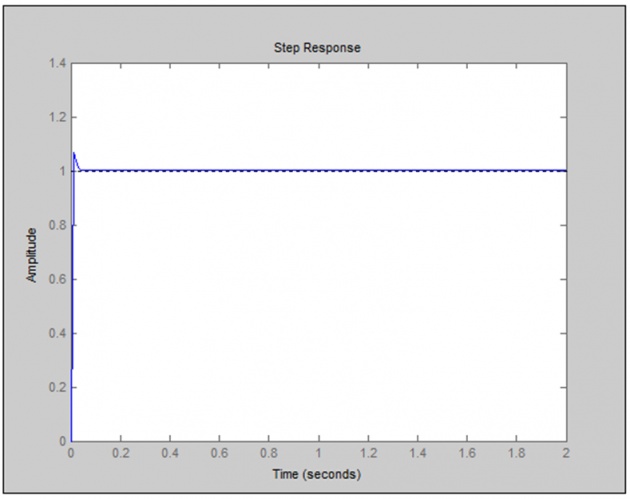
kp = 2.0

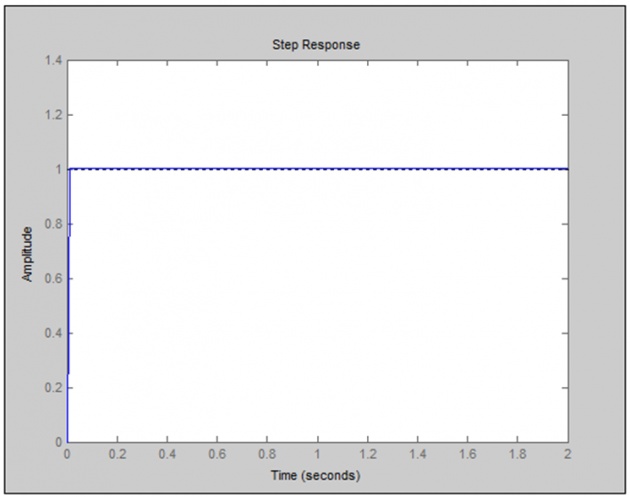
Observations

As we increase Kd from 0.1 to 0.9 to 2, overshoot of system is minimized, this concludes that increase in Kd of derivative controller can decrease maximum overshoot of the system, due to which damping effect is also minimized.

Conclusion

Suitable PID controller is with Kp=100, Ki=10 and Kd=2.
Results from figure 1 to figure 7 show that increasing values of K’s in PID controller can result in a better system than original.

We can see having figure 7 the last result to be the best with respect to minimum rise time, zero steady state error, negligible max overshoot and fast settling time.