Question No : 1

Solution:
First write make new file and save it with the name question_1.
function dxdt = question_1( t,x )
k = 1;
m = 10;
b = 0.5;
f = 1;
dxdt = [0;0];
dxdt(1) = x(2);
dxdt(2) = (f/m)-((b*x(2)/m))-((k*x(1))/m);
end
In the command window write question_1
X0=[0;0];
[t,x]=ode45('question_1', [0 250],X0);
plot(t,x)
title('Timpe Response')
xlabel('Time')
ylabel('Displacement')
grid on
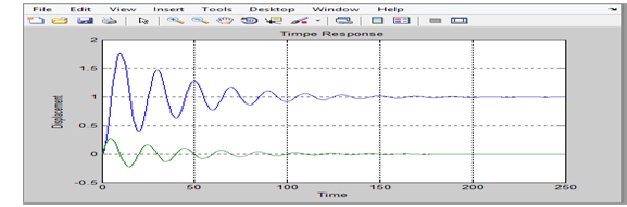
Clearly peak amplitude of the output is 1.8.
Now,in command window write the following
m=10;
k=1;
b=0.5;
num=1;
den=[m,b,k];
Transfer_fun=tf(num,den)
Transfer_fun =
1
------------------
10 s^2 + 0.5 s + 1
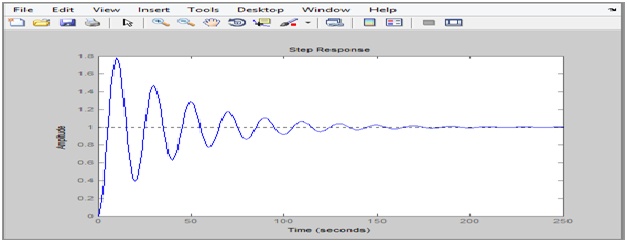
- Now we find unit step response of the above system
Step(Transfer_fun)
Question No : 2

Solution:
Open the matlab function new function file and write the following code Save it with the “question_1” name.
function dqdt = question_2( t,q )
vin=5;
R=10^5;
c=0.000002;
dqdt=vin/R-q/(c*R);
end
Now in command window.
[t,v]=ode45('question_2',[0,2],[0,0]);
plot(t,v)
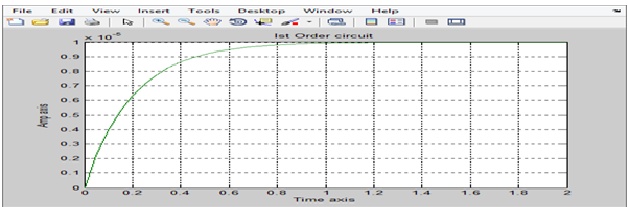
title('Ist Order circuit')
xlabel('Time axis')
ylabel('Amp axis')
grid on
Out Put :
Question No :3
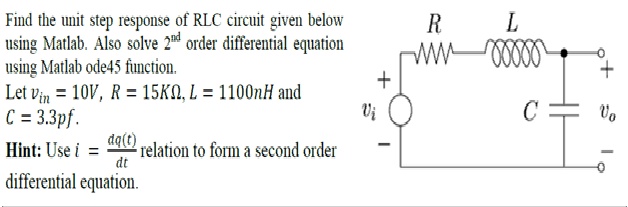
Solution:
Open the function file from matlab and write the following code and save it with “question_3”.
function dqdt = question_3( t,q)
vin=10;
R=15000;
L=1100*10^(-3);
C=3.3*10^(-6);
dqdt=[0;0];
dqdt(1)=q(2);
dqdt(2)=(-q(1)/(L*C))+(vin/L)-((R*q(2))/L);
end
Now in command window.
[t,v]=ode45('question_3',[0,2],[0,0]);
plot(t,v)
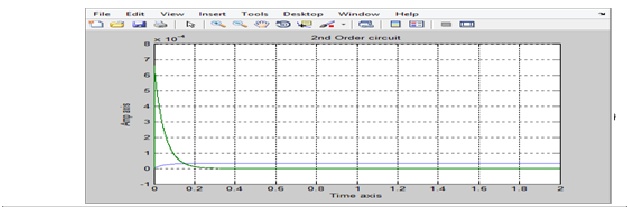
title('2nd Order circuit')
xlabel('Time axis')
ylabel('Amp axis')
grid on