1. Second order filter often referred to as Biquads.
2. Poles are complex conjugate in left half of the “s” plane and zeros are complex conjugate that may lie any where in ‘s’ plane.
3. It is to b remembered that:

 

T(s)=k(s+z1)/(s+p1)

Where           K=b1/a0        ,        z1=b0/b1 (zero)

 And               p1=a0/a1 (pole)

In s plane these two quantities are located at s=-z1,s=-p1

4. Pole,p1, will always lie on negative side of real axis
5. Zero may be either positive or negative part of real axis

 Design Parmeter “Q” and “Wo”:

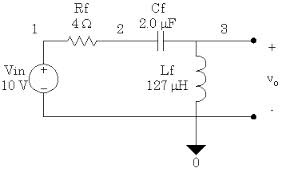
1. We begin with PLC circyit shown in figure which has new familiar form of a voltage divider. The transfer function of given circuit will be:

T(S) =VL(s)/V1(s)

2. The behaviourof the circuit at low frequency andhigh frequency is :

At low frequency, capacitoer behaves as open,then there is current in R, L and “c” circuit then

                        Vl=V1----approx equal

3. At higher frequency, capacitor will act as short, so that Vl approaches the value Vl=0

                   

3. From voltage divider :

  T(s)= Z2/(Z1 + Z2)

   This is the equation for second order circuit given above

                       T(s) = 1/cs/(R+Ls+1/cs) = 1/Ls/S(^2 + (R/L)s + 1/Lc)

5. The result may be put into tandard form by defining new quantites, we observe that when defining new quantity then circuit is lossless with R=0 then

          S^2 =1/Lc=0

6. S1,S2=+-j1/Lc =+-jW

    Mean poles are on imalnary axis and are conjugate axis.

7. For lossy circuit or coils, for  which a quality factor “Q” defined as Q/RLoss, which is the ratio of reactance at frequency “w” to resistance

   At Frequency                             

       w=w0

Q=WoL/R =1/R1/Lc

R/L=wo/Q

Put values of this equation in previous one, we get;

            T(s) = wo^2/(s^2+ (wo/Q)s +Wo^2)

8. The transfer function for low pass filter in this equation can be normalized form such that

           T(j)=1

9. Amore generalized form for T(s), in active circuit will recognize possibility of gain and also that, the associated circuit, may be inverting or no inverting

          T(s)=+-Hwo^2/(s^2 + (wo/Q)s + wo^2

    This can b represented as this diagram:

            

1.  Now we scale frequency by dividing  “s” by wo i.e., we use the normalized frequency, Sn=S/wo
2.             T(s)=+-H/(Swo)^2 + (1/Q)(S/wo+1)

                        =+-H/Sm^2+ (1/Q)(Sw0 +1)