PRINCIPLE OF STADIA SURVEY METHOD
The stadia method is based on the principle that the ratio of the perpendicular to the base is constant in all the similar isosceles triangles.
In actual practice, observations are made with either horizontal line of sight or inclined line of sight.
 In the later case, the staff may be kept either in vertical position i.e. upright or normal to the line of s

let two rays OA and OB be equally inclined to the central ray OC. Let A2B2, A1B1 and AB be the Staff Intercepts at the three positions C2, C1 and C, respectively. Now

       OC2/A2C2=OC1/A1C1=OC/AC

=CONSTANT=k=cot*beta/2

This constant k entirely depends upon the magnitude of the angle β.

Line of Sight is Horizontal and Staff is held Vertical:
Consider the above figure, in which O is the ‘Optical Centre’ of the objective of an external focusing anallatic telescope.
Let A, C, and B be the points cut by the three lines of sight corresponding to   the three stadia hair on the stadia hair-lineb, c, and a are the top, central and bottom stadia hairs of the diaphragm
ab = i = interval between the stadia hairs known as Stadia Interval
AB = S = Staff Intercept  
f = focal length of the objective
f1  = Horizontal distance of the staff from the optical centre of the objective
f2  = Horizontal distance of the cross-hair from O.
d  = Distance of the vertical axis of the centre of the instrument from O.
D = Horizontal distance of the staff from the vertical axis of the instrument.
M = Centre of the instrument just vertically above the instrument stationAs the rays BOb and AOa pass through the optical centre O, and they are the straight lines. So AOB and aOb are the similar s. Hence according to Law / Theorem of Similar Triangles:
Again, as f1 and f2 are the ‘Conjugate Focal Distances’.
1/f=1 /f2+1/f1
          
Multiplying throughout by f.f1, we get    f1 = f 1/f2*f+ f
Substituting the values of                    
f1/f2 = S/i
f1=S/i*f+f
Horizontal distance between M and the staff is D = f1 + d
D = f/i S + (f + d) = k S + C
 therefore, the staff intercept S is to be found out by subtracting the staff readings of the top and lower stadia hairs.
The constant k = f / i is known as the MULTIPLYING CONSTANT or Stadia Interval Factor and the constant f + d = C is known as the Additive Constant of the instrument.
Determination of constant k and C

First Method:

    In this method, the Additive Constant C = f + d is measured from the instrument
 

The distance d between the instrument axis and the objective is variable in the case of external . It should, therefore be measured for average sight. Thus, the Additive Constant f + d is found out.  
To calculate the Multiplying Constant k: Measure a known distance D1 and take the intercept S on the staff kept lat that point, the line of sight being horizontal

. Using the following equation:

            D1 = k. S + C        or          k = D1-C/S
    
For average value, staff intercepts, S1, S2, S3 etc., can be measured corresponding to the distance D1, D2, D3 etc., then the mean value is calculated.
Note: In case of external focusing telescopes, the eye-piece-diaphragm moves during the focusing. So, for such instruments, d remains the constant and does not vary while focusing.
Second Method:

    In this method, both the constants are determined by the field observations as under:

Measure a line about 200 m long, on fairly level ground and drive the pegs at almost equal interval, say 50 meters.

Finding the values of D and S for d by substituting the values of D and S in the equation of D = k.S + C. The simultaneous solution give the values of k and C; average of these are then found out.
For example, if S1 is the staff intercept corresponding to distance D1 and S2 corresponding to D2 we have,
                    D1 = k.S1 + C  . . . . . (i)           and      D2 = k. S2 + C   . . . . . (ii)
Subtracting (i) from (ii), we get:
K=D2-D1/S2-S1
Substituting the values of k in eq. (i), we get:
D1 =    D2-D1*S1 + C/S2-S1
Thus the equations (1) and (2) give the values of k and C..

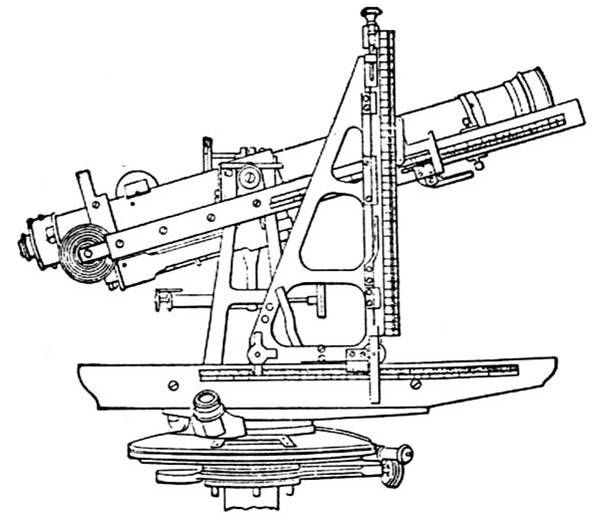
TACHEOMETRY
Staff is held vertical and Line of Sight is inclined to it i.e. LOS< staff
Inclined sight with vertical staff:

Let P = Instrument Station            Q = Staff Station

M = Position of instrument’s centre vertical axis    O = Optical Centre of the objective

A, C, B = Points corresponding to the readings of the three Stadia Hairs

S = AB = Staff Intercept                 i = Stadia Interval

L = Length MC measured along the line of sight

D = MQ = Horizontal distance between the instrument’s centre and the staff

V = Vertical Intercept at Q, between the line of sight and the horizontal line

h = Height of the instrument                       r = Central hair’s reading


 Angle AA’C = 900 + β/2, being the exterior angle of the ∆COA’.

 Similarly, from ∆COB’, angle OB’C = angle BB’C = 900 – β/2.
As β/2 is very small angle (its value is usually equal to 17’ 11” for k = 100), so the angle AA’C and angle BB’C may be approximately taken equal to 900
∟AA’C = ∟BB’C = 900
As the line A’B’ is perpendicular to the line of sight OC, equation D = kS + C
MC = L = k.A’B’ + C = kS.cosӨ + C           
Now the horizontal distance
        D = L.cosӨ = (kS.cosӨ + C).cosӨ
        
        D = kS.cos2Ө + C.cosӨ                          
Similarly,           V = L.sin Ө = (kS.cosӨ + C) sinӨ = kS.cosӨ.sinӨ + C.sinӨ
V = kS. sin2Ө + C.sinӨ   = ½ kS.sin2Ө + C.sinӨ       
                                              
Thus the equations (1) and (2) are the formulas to find out the horizontal distance D and elevation V for the inclined line of sight.

As the telescopes mostly used in Tacheometric Surveying are the External Focusing Telescope with anallatic lens, and the Additive Constant C is taken as zero in this type of telescopes. So, whole the term Ccos becomes zero in the equation of D = kS.cos2 + C.cos
So it becomes D = KScos2   [In internal focusing telescope, the term Ccos becomes so small that it can be neglected, hence making the above equation same as D = kScos2 and V = ½(kSsin2)
Elevation of Staff Station for Elevated Angle i.e. Elevated LOS:
E = RLEq.St + h + V – r

Reduced Level (RL or R.L): It is the height or depth of a point above or below a Datum. Generally, Reduced Level is known as Elevation of a point.
Datum: It is any level i.e. elevation of a surface with respect to which the levels i.e. elevations of other points or surfaces are measured or referred to. These are usually the Mean Sea Level (MSL) or Bench Mark (BM) or any arbitrary point or surface of known elevation.

Elevation of Staff Station for Angle of Depression i.e. Depressed LOS:

E = RLEq.St + h – V – r

Case (a): When the Line of Sight is at an elevated angle of Ө:

Let AB = S = Staff Intercept

    CQ = r = axial hair reading

    With the same notations , we have:

                MC = L = kS + C

    
D = MC’ + C’Q’ = L.cosӨ + r.sinӨ
    = (kS + C).cosӨ + r.sinӨ
Similarly,     V = L.sinӨ = (kS + C).sinӨ
Case (b): When Line of Sight is at an angle of depression Ө

 the line of sight depressed downwards
MC = L = kS + C
       D = MQ’ = MC’ – Q’C’
                  = L cosӨ – r sinӨ
           D = (kS + C) cosӨ – r sinӨ
  V = L sinӨ = (kS + C) sinӨ

Elevation of Q = Elevation of P + h – V – r cosӨ